Thursday, November 19, 2009
TIPS AND HINTS
Thursday, November 12, 2009
Logarithm and inverses
- there can not be an inverse without an original function
- i have learned that in order to find the inverse of a graph, we switch the input and output of the original graph. here's an example:
- f(ƒ−1(x)) = ƒ−1(f(x)) = x
- how to graph log.. uh huh. thats right. not at all.
- i also do not under stand how to find x in a case like this: ln (y-1) - ln 2 = x + ln x
Wednesday, November 4, 2009
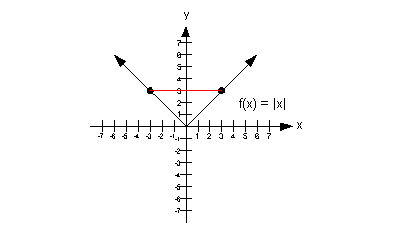
EVEN and ODD Functions
A function is even if replacing x with -x does not change the original function.
The graph of an even function is symmetric about the y-axis.
Since f(-x) = f(x); point (x,y) share the same y value as point (-x,y).
example:
*notice points (3,3) and (-3,3) and also note how it is symmetric about the y-axis.
ODD FUNCTION
A function is odd if replacing x with -x results in changing all terms of the original function. The graph of an odd function is symmetric about the origin(0.0).
Since f(-X) = -f(x); point (x,y) lies on the graph only if (-x,-y) lies on the graph.
example:
* Note how it is symmetric about (0,0)
*Figure 5 is an Even Function, Figure 6 is an Odd Function
Tuesday, October 27, 2009
About Me
Hello.
My name is Wanasanunt On-art; "Wendy" or "Kai". Most people at school know me as Wendy. But honestly, I prefer Kai. Kai is short for "Prakai" in thai meaning sparkly and shiny things; it can also mean spark or lightning.
My nicknames were given to me by my father. Both Wendy and Kai.
But i prefer Kai because it has a nice meaning while Wendy is just an English name since the early 1900s that sounds cute and is certainly easier to pronounce than Wanasanunt. My dad said he liked Peter Pan so that was the start of the name "Wendy Darling."
I am 17 years old. I have a lot of pride in my class of 2011. I am Junior. And also Junior class A-track Vice President. Now you know why I have so much pride. I also have a lot of pride in the Advantage Plus Program. It ticks me off when I hear people say that Magnet is better, I'd turn around and SNAP!!!! I believe that our APP is the best and we accelerate faster than any Magnet student on Campus. But that5's just my opinion. (Which will be soon proven a fact!!!)
I love rainy days the most. Because I love my boots. My boots are comfy. I even wear them on non-rainy days. And rarely on hot summer days. I am obsessed with shoes. Well maybe obsessed might not be the right word to use, but let's put it this way, I like shoes. But at the moment I am just too broke to buy a new pair every week or two.
Although I love rainy days, I do feel that they are quite gloomy and it tends to ruin people's moods. Sunshiny days are nice sometimes. Just SOMETIMES.
I loves swimming in the summer. Dipping my toes into the cold pool. Often too cold. But it's alright.
I love to Sample food!!! A lot of FOOD!!!


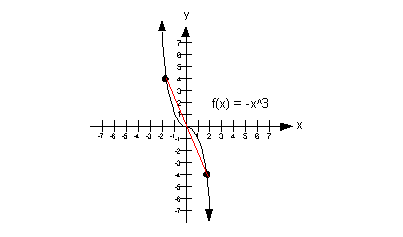
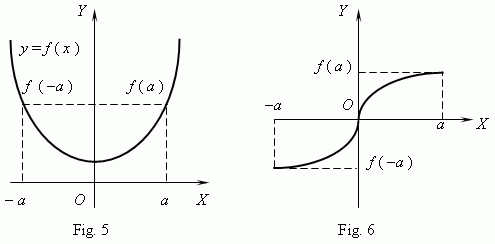
.jpg)